triangulum
pseudo-aperiodic tilings on a triangular grid
Inspired by the discovery of the aperiodic Hat- and Spectre-Einstein-tiling I programmed my own pattern generator. The aim was similar: To test some pseudo-aperiodic patterns and additionally, to display some with self-complementing tiles.
First I set up a triangular grid with simple shapes, made out of two or twelve triangles: a diamond and a dekagon (the latter in form of two combined hexagons).
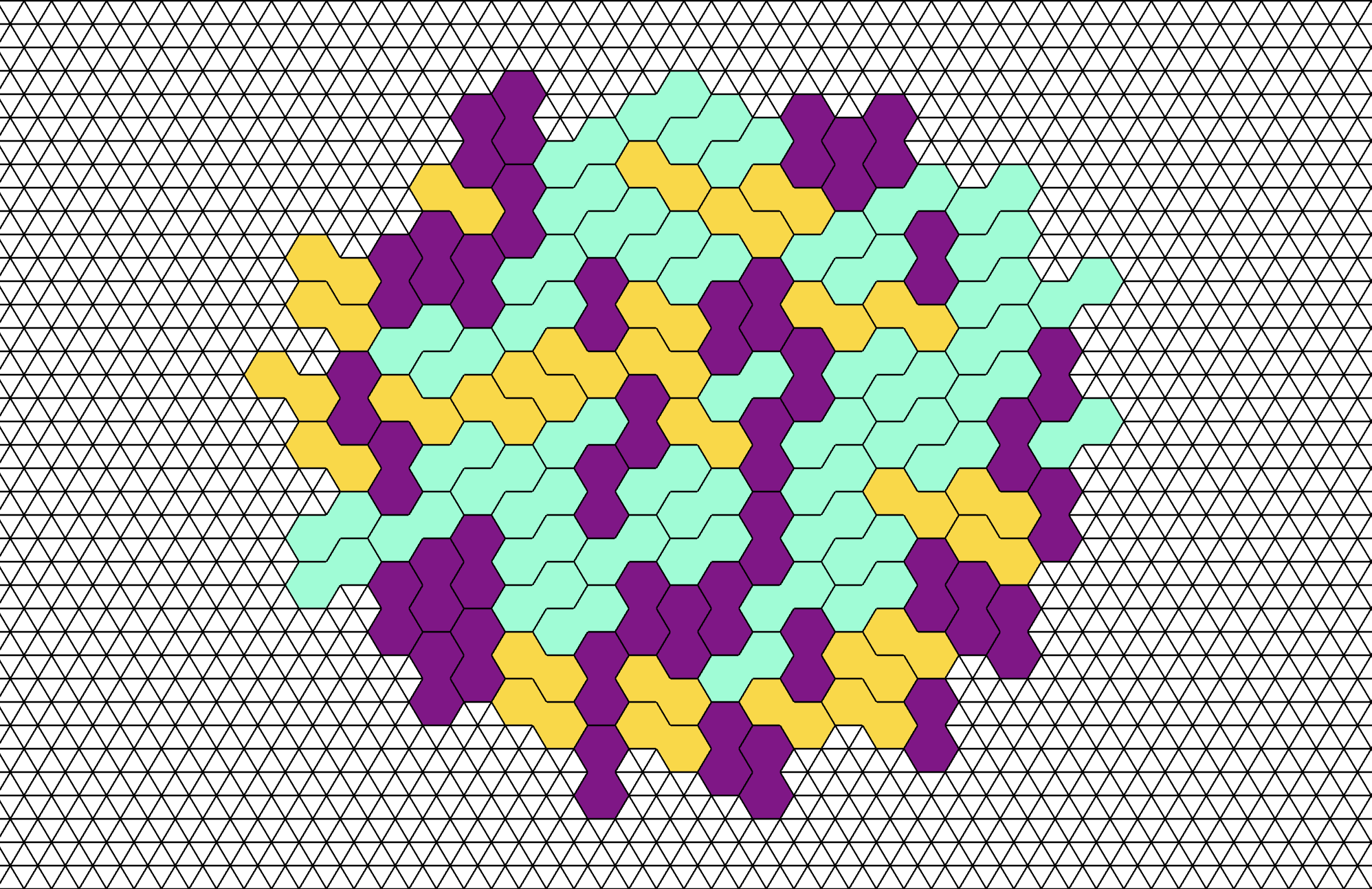
pattern of simple dekagons, coloured according to orientation
To vary the visual effect, the algorithm of placing the tiles starts in the center and uses random choices to place the next tiles around it.
So, these patterns out of dekagons can be aperiodic when laid, while the tiles itself do not follow the rule strictly: To enforce aperiodicity by default in the laying-process.

dekagon-m-1

dekagon-m-2
dekagon-m-3
Visually I found it much more interesting, when these dekagons are composed out of two identical smaller tiles, which can fit right into each other. Being set within the triangular grid, these self-complementing tiles consist of 24 triangles and form the dekagon with 48 triangles, when complemented.

self-complementing tiles, which always contain two colours in one dekagon